
represent 하는 state는 2^n 개이지만 joint pdf 를 나타내기위한 필요한 parameter 개수는 2^n-1 이다.
마지막 1개는 1- (the other parameter's probabilty)를 해서 계산할 수 있으니까

but when assuming RV are indepdent variable. we can calculate joint distribution by mulitpling each pd
and then we only need N parameters , since we know how to calculate joint distribution.
before example we didn't know how to calculate joint distrubiton so we literally need P(X1, X2... Xn) for every iteration of combination
목표는 parameter 개수 줄이기가 목표이다.

we can assume Chain rule at any given situation. basically saying,
the probabilty of bunch of events happening at the same time ==> as a product of conditional probabilities.
bayes' rule is corollary of chain rule

without any assumption at chain rule , # of parameters are still same
but when we assume Xi only need previous Xi-1, we need 2n-1 parameters
1 + 2 + 2+ 2.. = 2n -1


DAG는 toplogy sort 를 통해 일정한 순서로 정렬할 수 있고 정렬한 CPD에 chain rule을 가할 수 있다.
이렇게 그래프로 표현하면 parameter 개수가 좀 더 줄어든다.

Grade같은 경우에는 Pa(parent) 에 영향을 받기 때문에 표현식이다르다.
joint distribution 을 전체를 표현할 때 letter 같은 경우에는 Grade의 probabiltiy만 알면되고 그 밑에것 까지 계속해서 알 필요는 없어서 parameter 수가 현저히 줄어들게 된다.

Difficulty 랑 intelligence랑 indepdent하고 Letter는 Intelligence, Diffculty, SAT랑 indepentedent 라고 가정하면
저위의 그래프가 나오는것이고 2번째 식을 1번쨰 식처럼 줄일 수 있게 된다.
X는 word들이고 Y는 email 안에 들어있는 word를 기반으로 spam 인지 아닌지 구분하는 label
discriminative model 은 given xs' 에서 Y를 추론하는것이고
generative model은 given Y에서 given x들을 추론하는 것이다.

Logistic regression is way of modeling conditional distribution of Y given xs.
위에서는 DAG로 condition들을 표현했지만 그것보다 더 수월하게 아예 Logisitic 한 함수로 관계를 정의해서 표현한것이다.
즉 좀더 loose하게 X들의 condition을 정의한것이다. 이러면 좀 더 일반적인 상황에 잘 맞고 model로 하여금 더 많이 배우게 할 수 있다고 한다.
기존의 bayesian 들과 다르게 joint distribution에 대한 고민을 하지않음 즉, x에 대한 distribution을 고민하지 않는다.
어차피 inference time에는 뭔 x가 오는지 알 수 없기 떄문에 P(Y | X)의 distribution만 고민한다.
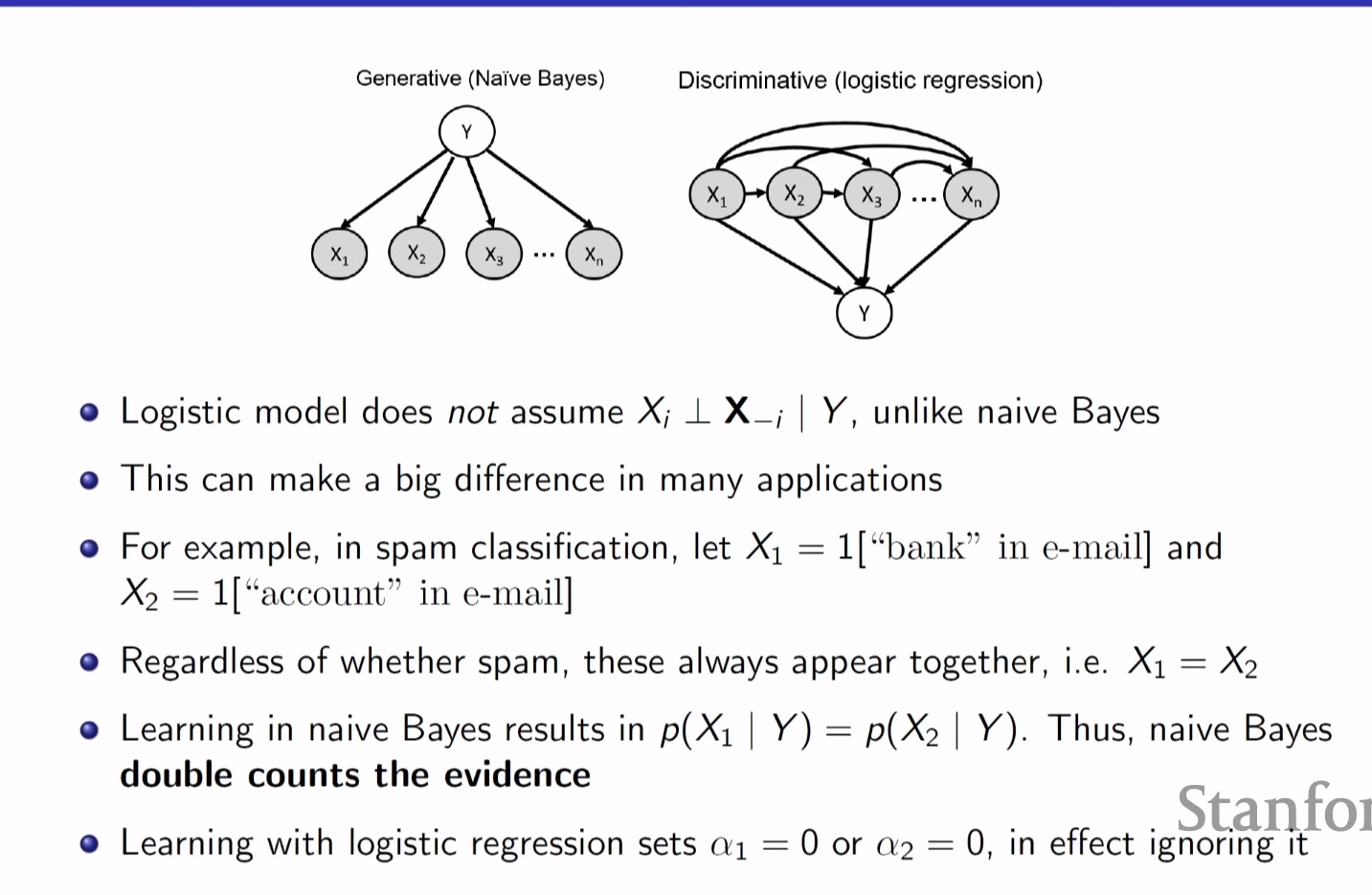
Navie Bayes는 X들이 싹다 independent 하다고 생각하기 때문에 bank , account를 2번 다 spam label에 도움이 된다고 생가하지만 logisitic은 그렇게 하지 않고 1번만 count할 수 있다.
discriminative 는 x가 없으면 무용지물이다. generative는 joint distribution , 즉 전체를 알려고하는 것이기 때문에 좀 더 광범위 하게 쓸 수 있다.

그냥 linear하다고 가정하지않고 좀더 loose하게 Ax+b == h (non-linear)로 가져간다. 이걸 stacking하면 NN이 된다.

복잡했던 conditional distribution을 그냥 NN에 맡긴다.

Z-> X은 Bayesian network일 때 각 distribution을 가정한것이다.
마지막은 Z를 gaussian 에서 sampling하고 그것을 NN에 넣어서 mu , theta를 계산한후에 그것을 기반으로 gaussian distribution을 만들고 X를 sampling할 수 있다.
'AI > Stanford CS236: Deep Generative Models' 카테고리의 다른 글
| Lecture 7 - Normalizing Flows (0) | 2024.05.26 |
|---|---|
| Lecture 6 - VAEs (0) | 2024.05.23 |
| Lecture 5 - VAEs (0) | 2024.05.21 |
| Lecture 4 - Maximum Likelihood Learning (0) | 2024.05.19 |
| Lecture 3 - Autoregressive Models (0) | 2024.05.18 |