
G(s) 를 보고 2차 미분 방정식으로 이루어진 LTI system임을 알 수 있어야 한다.

기존에는 x(t) 가 input 이였다. 하지만 state space에서는 X(s)를 state 으로 쓰기 때문에 U 를 input으로 notation이 바뀐것이다.
그래도 햇갈린다. x(t) 를 L transform 한것이 X(s) 이긴한데.. X(s) == U(s) 는 아닌데..
X(s)는 state에 따른 값이고 U(s) state에 다른 input인데 (초기값과 비슷한역할인것 같은데)
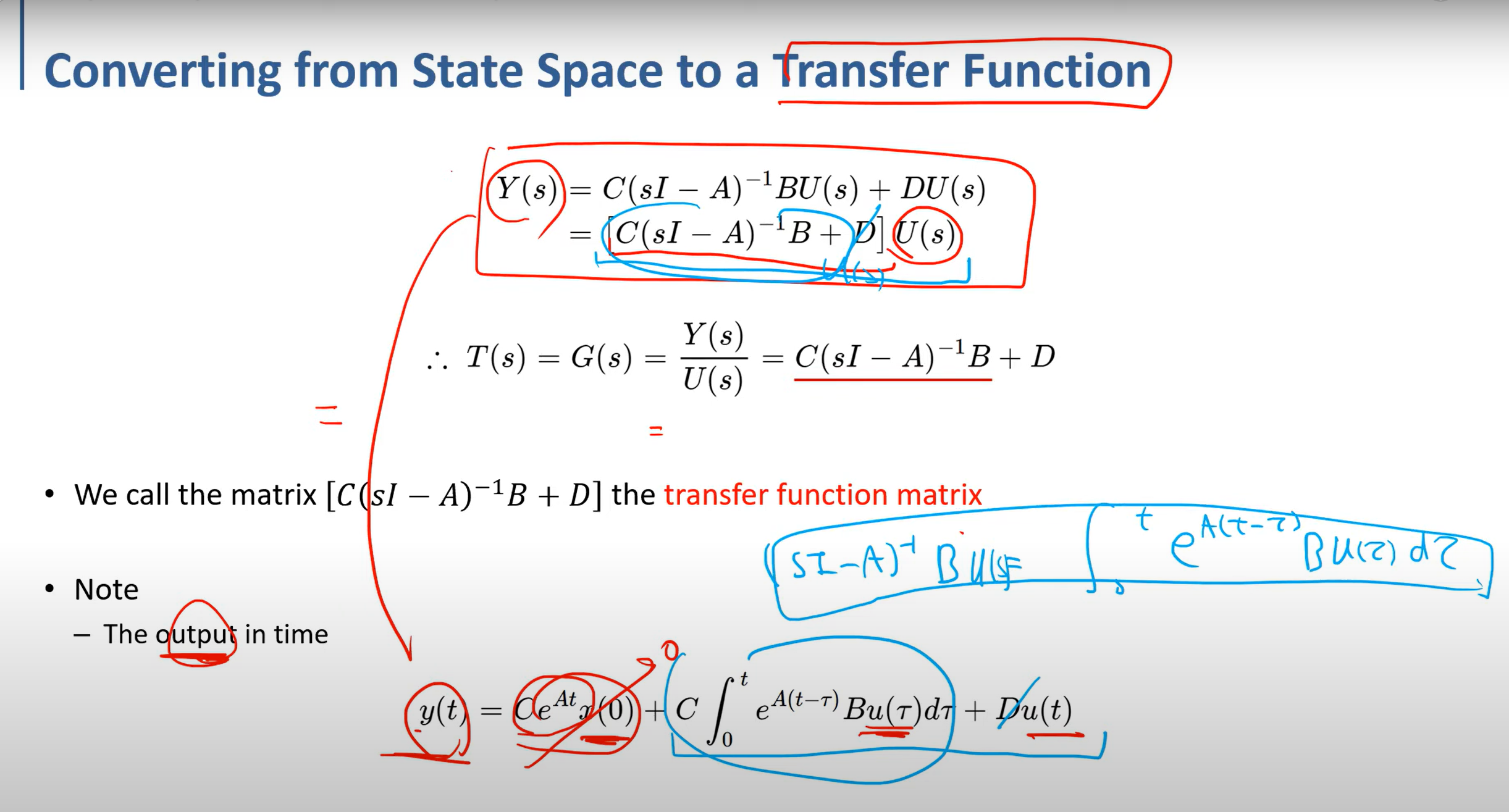
transfer function을 구할 때는 초기 값을 0이라고 가정한다. 순수하게 input에 대한 output만을 구하고 싶기 때문에
system이 stable하다면 Ce^At가 0에 수렴한다. stable 하면 A가 음수라 0으로 수렴하게 된다.
이때 파란색으로 써놓은식이 서로 같다는것을 보이고 싶다.
즉 L transform해서 구한 Y(s)랑 ode를 풀어서 나온 y(t)가 같다는것을 보이고 싶은것이다.
'AI > Dynamical Systems (동적시스템)' 카테고리의 다른 글
| 06 state space 02 (상태 공간) (0) | 2024.03.10 |
|---|---|
| 06 state space 01 (상태 공간) (0) | 2024.03.10 |
| 05 Laplace transform 03 (라플라스 변환) (0) | 2024.03.02 |
| 05 Laplace transform 01, 02 (라플라스 변환) (0) | 2024.02.20 |
| 04 forced response 09 (강제 응답) (0) | 2024.02.10 |