
state equation에 들어가는 함수는 보통 general 해서 non linear 할 수도 있지만 여기서는 linear한 범위만 다룬다.

A matrix는 LTI system에서 state 의 dynamics를 u는 input을 나타내는 것이다.

y(output response에서) C x 는 LTI system의 영향도를 D u는 input에 대한 영향도를 의미한다.
보통 D가 0인 경우가 많다.

예를 들면 state variable은 position , velocity가 될 수 있다.
LTI System을 standard state space form으로 나 타낼수 있다. 또한 block diagram을 따라가 보면 standard form을 그림으로 나타낸 것이다.
미분기는 noise같은 값들이 증폭되는 경향이 있기 때문에 system 을 구성할 때 보통 사용하지 않는다. 적분기는 smoothing 효과가 있어서 오히려 noise를 줄이는 경향이 있어서 많이 쓰인다.

homogeneous는 input이 zero인 경우이다. 기존의 first order ode의 해를 구하는 것과 동일하다.
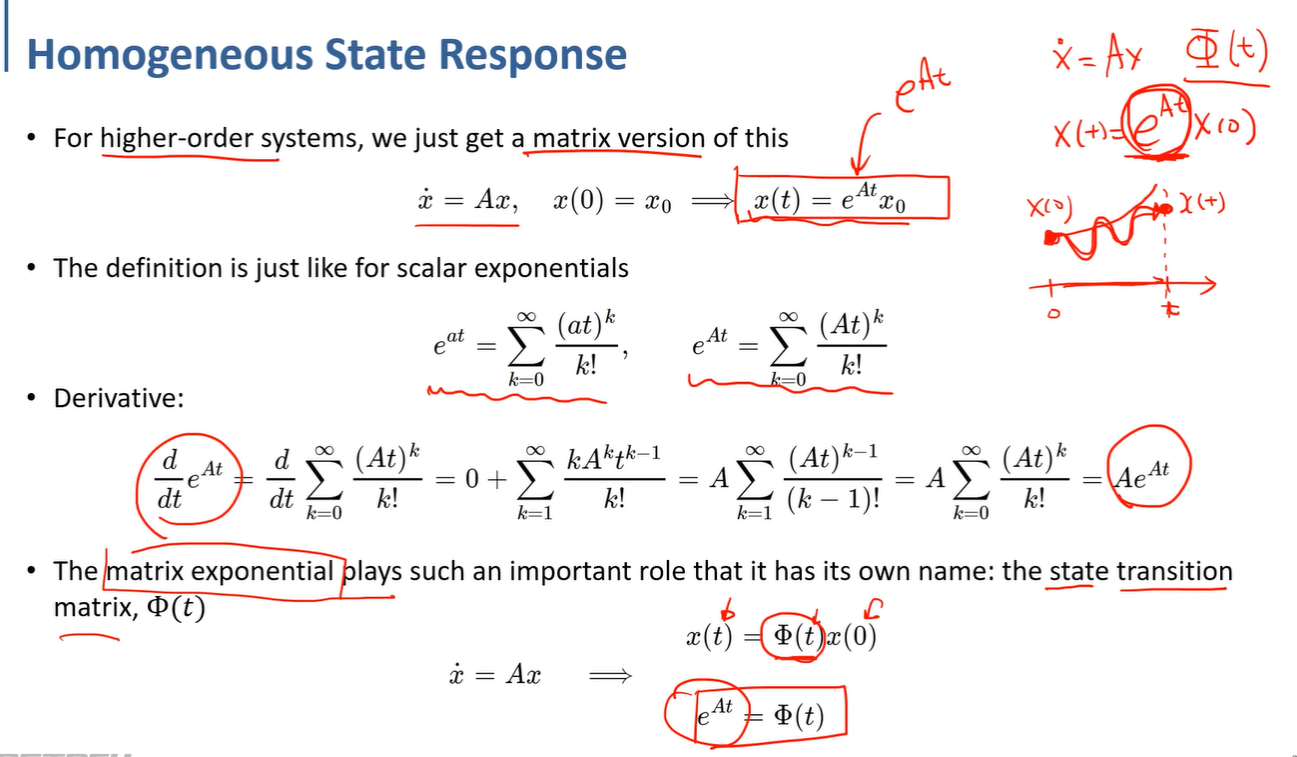
pie(t) 는 실제로는 exponetial matrix이지만 이 값을 해석할 때는 주어진 init condition x(0)에서 t 만큼의 시간이 흘렀을 때의 x(t) state를 나타내게 해주는 state transition matrix라고 해석을 한다.
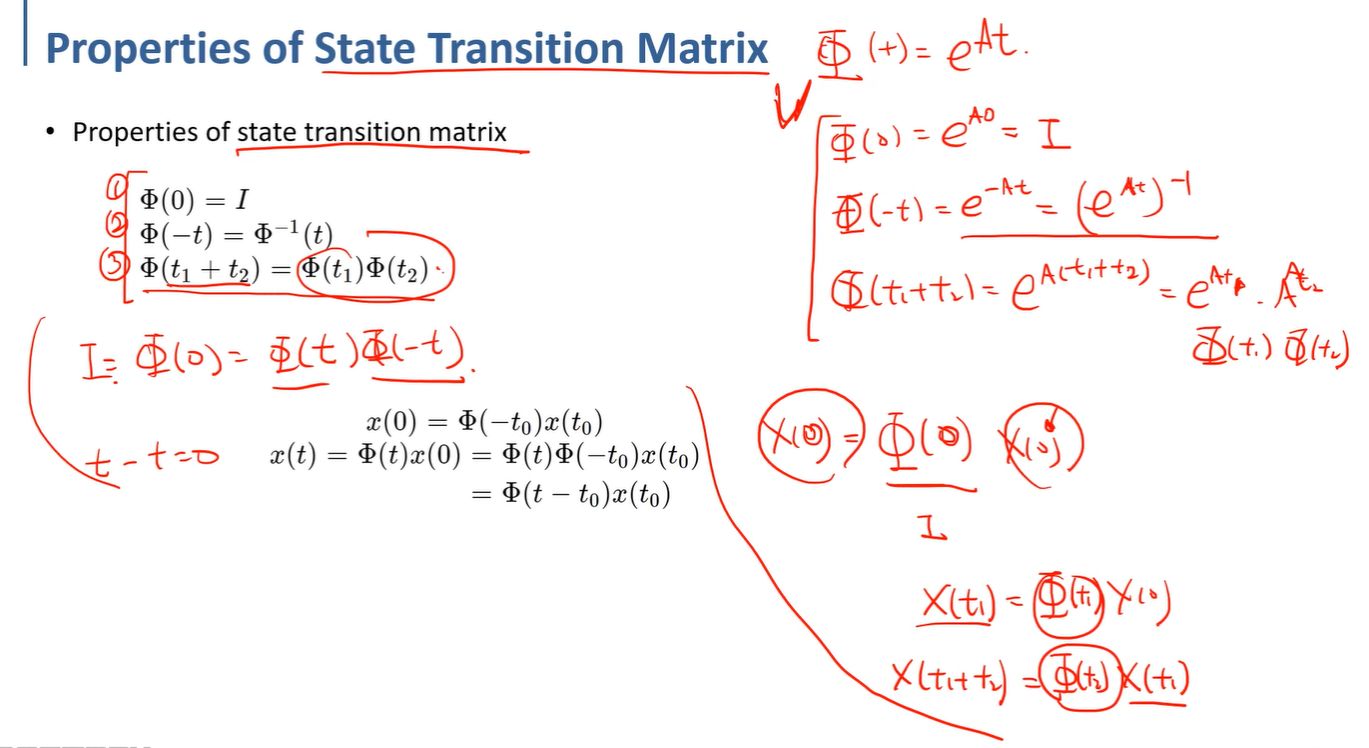
pie(0) 의 의미는 I가 되어야한다. 실제로 x(0)에서 pie(0) 만큼 transit 시키면 동일한 상태이어야 하기 때문이다.
pie(t1 + t2) = pie(t1)pie(t2) 는 x(0)에서 pie(t1) 만큼의 시간이흐른 x(t1)과
x(t1+t2) = pie(t2)x(t1) 이기 때문에 성립한다.
pie(t)pie(-t) 의 의미는 x(0) = pie(t)pie(-t)x(0) 일 테니 I가 된다. 즉 서로 역행렬의 관계인것을 알 수 있다.
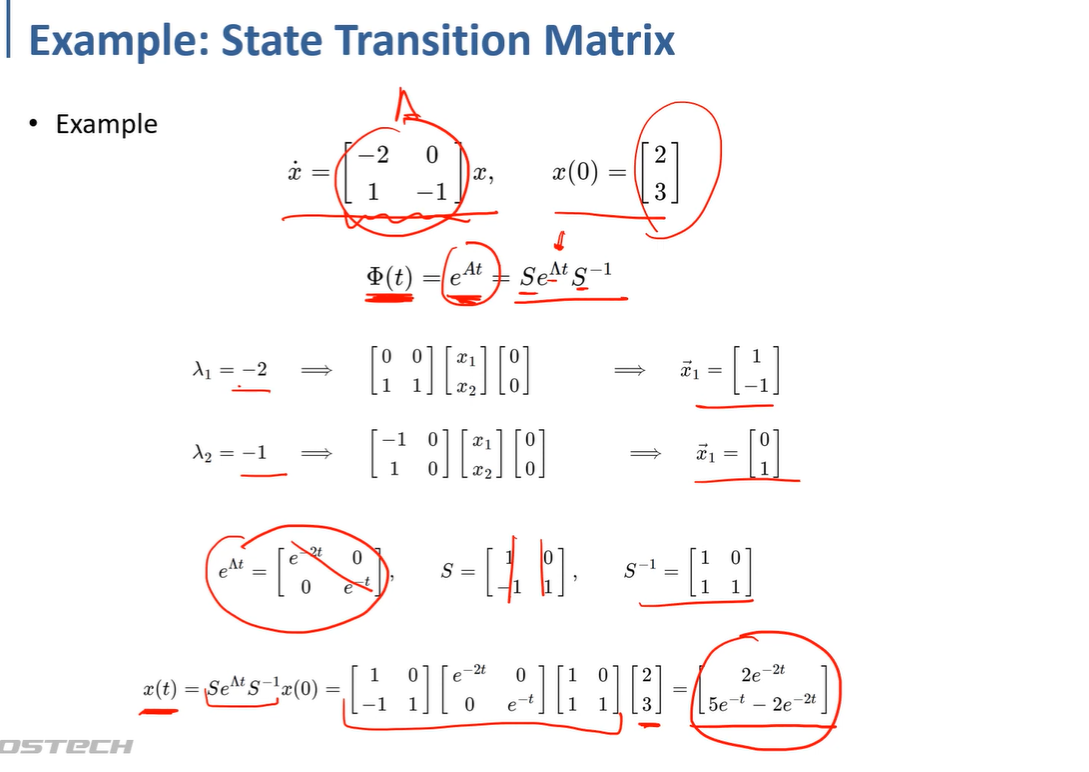
x' = Ax + Bu
y = Cx + Du
로 나타낼수 있는데 현재 주어진 input이 0 인 homogenous한 LTI system을 다루고 있으니 B, D == 0이다.
x(t)를 구하기위해서 ode를 풀면 된다. 이후 output인 y를 구하기 위해서 C x를 하면 된다.
보통 C는 I (1 diagonal matrix)인것 같다.
'AI > Dynamical Systems (동적시스템)' 카테고리의 다른 글
| 07 rep LTI 01 (선형 시불변 시스템 표현) (0) | 2024.03.15 |
|---|---|
| 06 state space 02 (상태 공간) (0) | 2024.03.10 |
| 05 Laplace transform 03 (라플라스 변환) (0) | 2024.03.02 |
| 05 Laplace transform 01, 02 (라플라스 변환) (0) | 2024.02.20 |
| 04 forced response 09 (강제 응답) (0) | 2024.02.10 |