
<b1 , b2> 는 b1, b2 vector의 내적을 의미한다.
c_i 는 x가 b_i를 얼마나 가지고있는가 를 의미한다.
c_i를 나태내는 분모의 값 (b_i, b_i) 는 normalization factor라고 생각하면 된다.

H(jw) 는 fourier series에서 각 harmonic component의 계수를 의미했었다.
현재 x에 e^jwt 가 얼마만큼 분포 해 있는 지 구하기 위해서 내적을 한 결과가 결국 x를 fourier transform 한 결과라는 것을 의미한다.

Fourier transform 은 laplace transform의 special case이다. imagnary 영역 (compelx) 만 고려할 때 사용되는 개념이다.
즉 s = jw (complex) 일 때 적용된다.
laplace transform을 나타낸 평면은 e^-st를 basis 로 한다함 (잘 이해가안감)
제1 사분면은 반시계 방향으로 회전하면서 점점 amplitue가 커지는것이고
제2 사분면은 반시계 방향으로 회전하면서 점점 amplitude 가 작아지는 것이다.

기존에는 omega(각속도) 만 값이 변화가 있었다. 즉 복소 평면에서는 y축에서만 변동이 있었던것이다.
laplace transform에서는 sigma(실수부분)도 변하니 복소평면 전방향에서의 변동을 의미한다.
s 변수는 실수부분 + 허수부분으로 이뤄졌으니 좀 더 general 한 variable 을 의미한다.

input이 e^st 로 주어졌을 때 기존의 LTI output response를 구하듯이 convolution을 하면 e^st * H(s) 가 나온다.
H(s) 는 laplace transform을 한 결과 값이고 eigen value역할이다. 또한 e^st는 여기서 eigen function역할을 하게 된다.
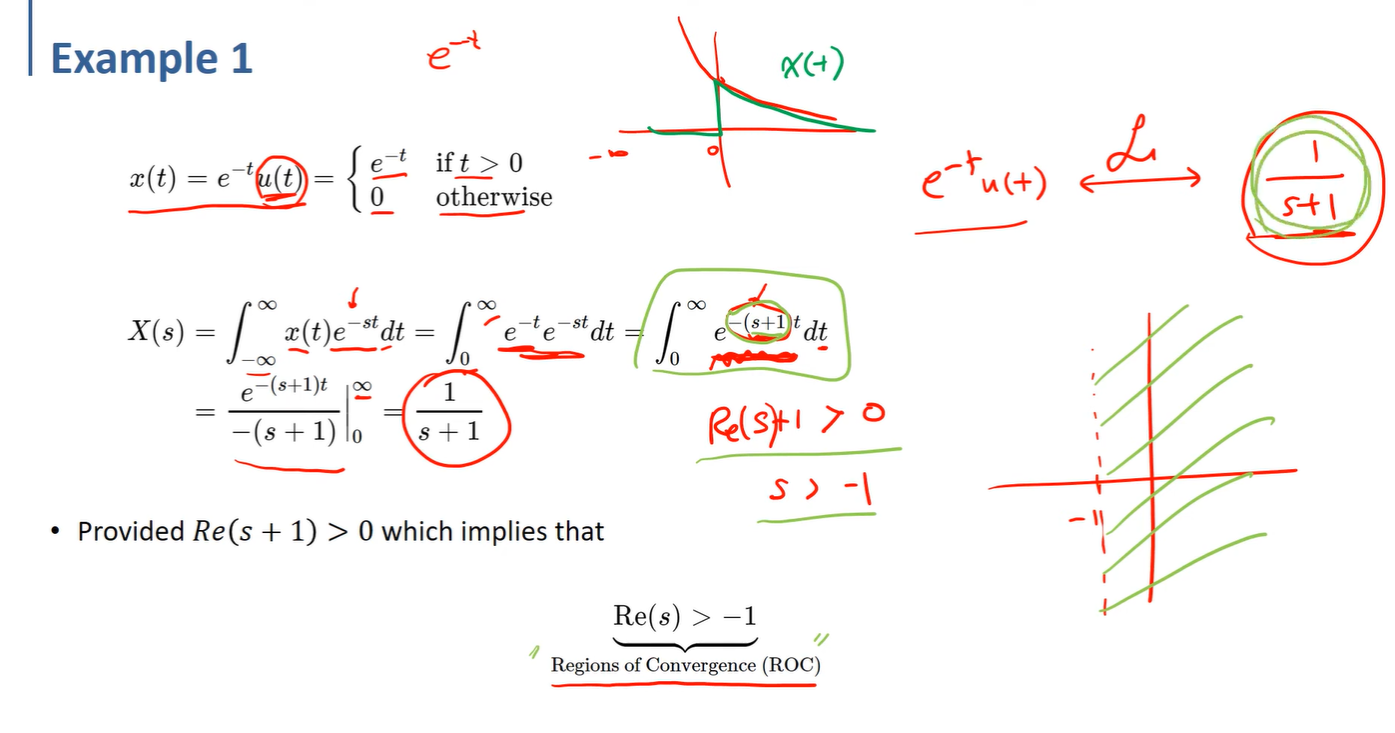
예시를 lapalce transform 을 가했을 때 적분을 해야하는 값의 실수부가 -1보다 커야 converge하게 된다. 이를 ROC, 즉 실수부가 -1이상인 영역에서만 laplace transform 한 결과가 정의가 된다는 의미이다.
e^(양수) 이면 0~inf 까지 적분을 하게 되면 무한으로 발산하게 되니까
또한 transform한 결과 값을 보고 원형을 유추할줄 알아야한다.

그러면 항상 수식을 써서 계산하는 것이 아니라 이미 구한 결과값으로 transform한 결과를 구할 수 있다. laplace transform이 linear하다는 특징을 이용해서 구한것이다.

dirac function의sifting property 때문에 곱한후에 L transform 을 하면 1이 된다.
이를 그림으로 이해하려면 기존의 F transform 은 impulse input diract이 들어왔을 때 omega domain에서 모든 값이 1이었다면
L transform은 S domain에서 전영역이 1인것으로 이해할 수 있다.
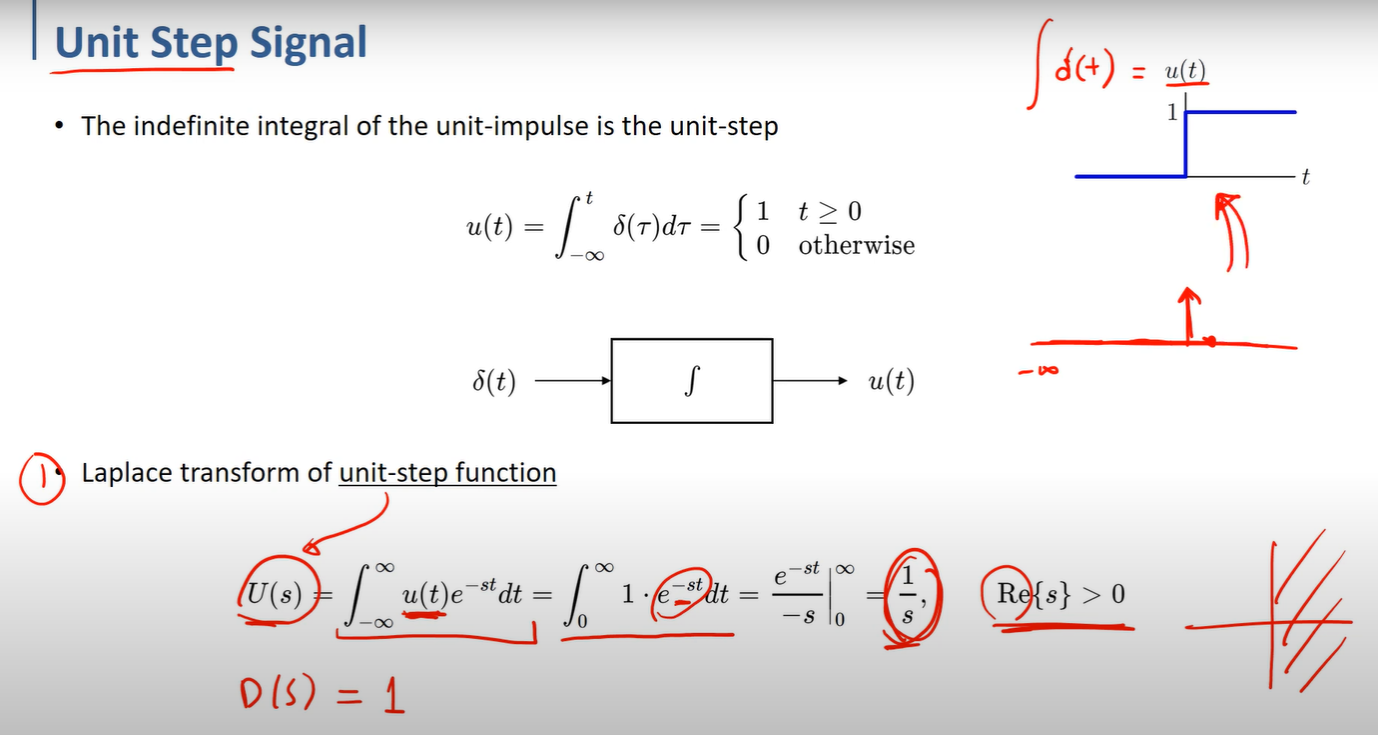
unit step function을 L transform 한 결과와 dirac 을 L transform 한 결과이다.
또한 dirac 과 unit step 의 관계는 적분으로 이루어진다. -inf~ 0까지는 적분값이 0이 어었다가 0을 지난 후에는 1이 추가되니 계속 1의 값이 나오게 된다.
'AI > Dynamical Systems (동적시스템)' 카테고리의 다른 글
| 06 state space 01 (상태 공간) (0) | 2024.03.10 |
|---|---|
| 05 Laplace transform 03 (라플라스 변환) (0) | 2024.03.02 |
| 04 forced response 09 (강제 응답) (0) | 2024.02.10 |
| 04 forced response 08 (강제 응답) (1) | 2024.02.06 |
| 04 forced response 06 , 07 (강제 응답) (1) | 2024.02.03 |