Fourier Transform

w = kw0 , dw = w0 인 이유는 T가 무한으로 가면 w0 가 dw 가 되기 때문이다. (아주 작은 delta가 됨)
이떄 k 는 정수배를 의미하는것이다.
X(jw) 는 크기 + phase 를 , e^jwt 는 compelx harmonic 즉 주기를 의미하게 된다.
aperiodic input은 기존 periodic input과 다르게 discrete harmonic compoenent 로 이뤄지는게 아니라 continous , 즉 모든 frequency로 이뤄진다고 볼 수 있다.

anaysis 부분은 위 공식에서 e^jwt, e^-jw't 의 곱연산중에 w==w'이 되는 순간에만 주기함수의 적분할때 0이 되는것에서 살아남음을 표현한 것이다.
w == w'이면 exponetial 부분이 0이 된다.
synthesis 와 analysis (통합 , 분해 ) 에서 w에 부호가 다른이유가 될 것이다.
X(jw) = harmonic component의 크기 + phase를 통해 e^jwt = eigen function (일정한 주기) 들의 곱을 더하여 reconstruction한 것이 synthesis이다.

analysis 부분을 살펴본다.
내적은 각 벡터의 유사도를 따질 수 있는 index이다.
functional space에서 내적은 complex conjugate를 곱하고 t에 대해 적분하는것 == x(t) * y^*(t)
그러면 analysis에 적분 대상은 사실 <x(t) , e^jwt> 로 functional space에서의 내적이라 볼 수 있다.
이것이 의미하는바는 x에서 y의 component 가 얼마만큼 차지 하는지? 를 의미한다.
즉, x(t) 에 e^jwt 의 eigen function을 가지는 component 가 얼마만큼 있는지 계산하는것이고 그것이 X(jw) 로 나타내진다.
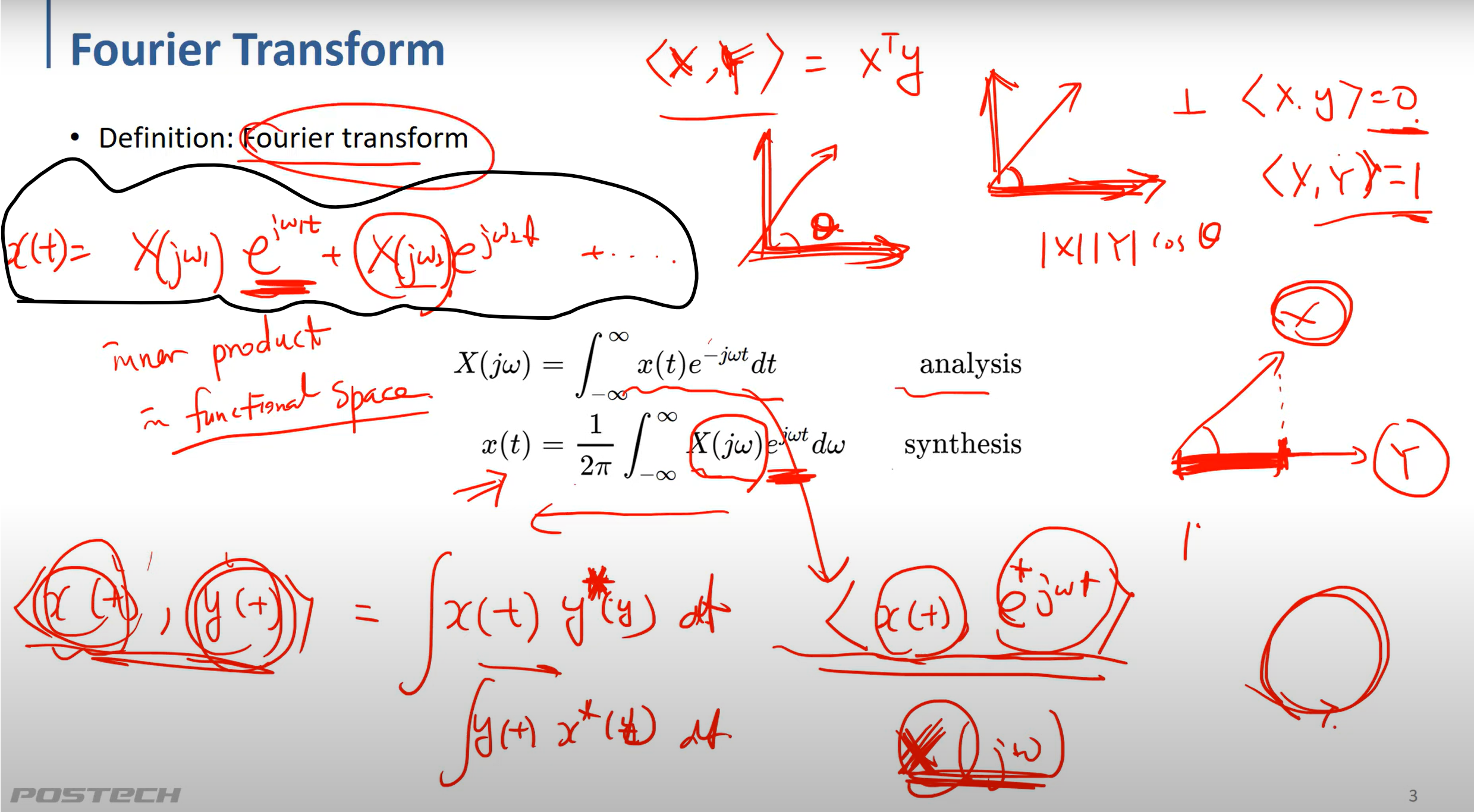
예를 들면 synthesis를 할때 e^jw1t 의 양이 X(jw1)만큼 있다. 이런식으로 phase + amplitutde를 나타내준다.
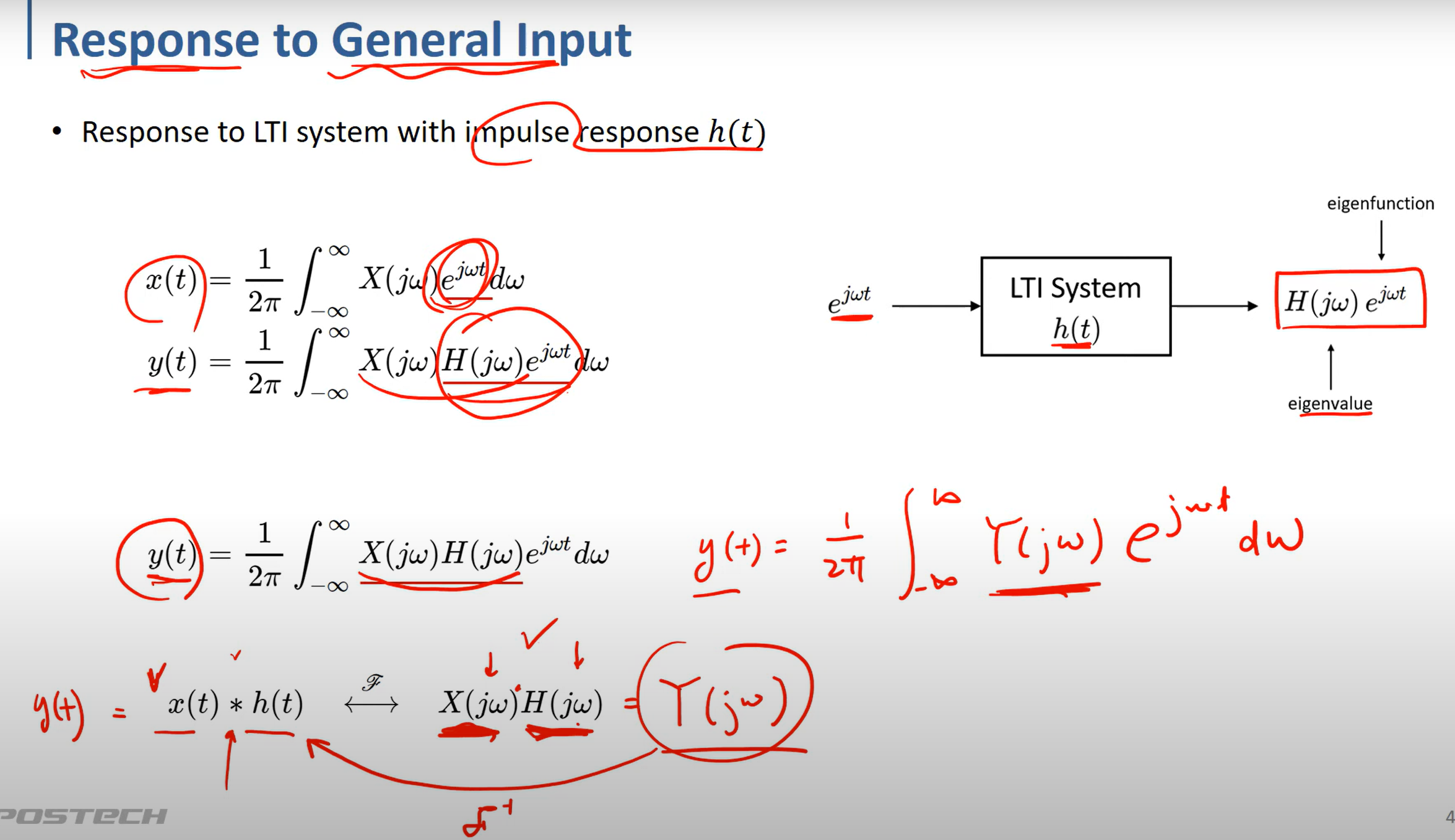
y(t) 는 x(t) * h(t) 의 convolution으로 계산이 되었지만
Y(jw) , 즉 y(t)의 fourier transform의 결과 값은 x(t) , h(t) 각각의 FT 한 결과값을 곱하면 된다.

dirac delta function을 fourier transform 하면 모든 frequency domain에서 1의 값만큼을 가지고 있다.
delta function과 h(t) [LTI system] 의 convoluation을 한 값은 h(t)로 나오고
Fourier transform 한 결과 값의 곱도 1 * H(jw) = H(jw) 로 그대로 나오게 된다. 이게 magic이라는것 같다.
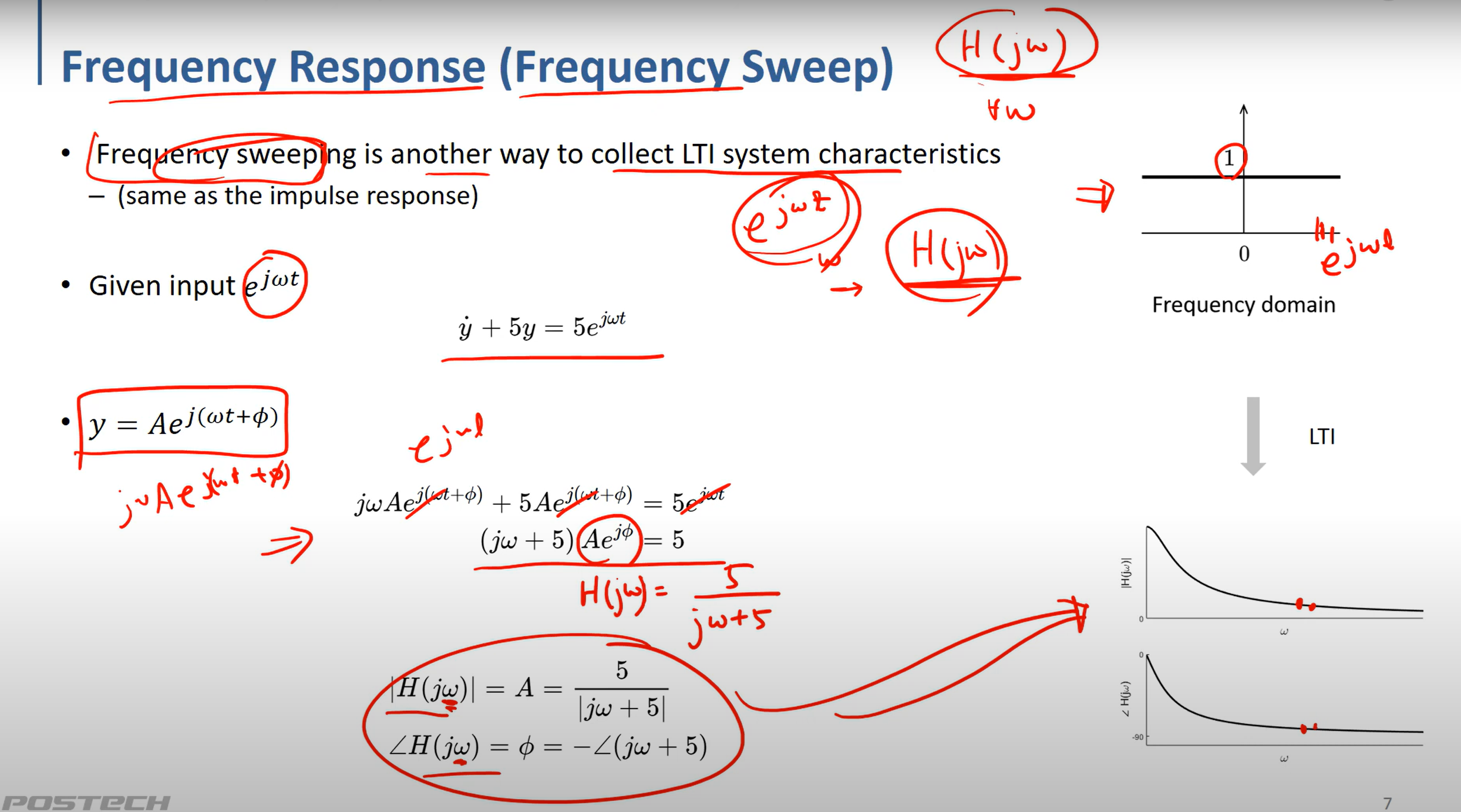
frequency response [H(jw)] 를 구할 때 impulse input을 줘서 구하는 방법과
직접 e^jwt input을 가정하고 식을 계산해서 H(jw)를 구하는 방법이있다.
'AI > Dynamical Systems (동적시스템)' 카테고리의 다른 글
| 05 Laplace transform 03 (라플라스 변환) (0) | 2024.03.02 |
|---|---|
| 05 Laplace transform 01, 02 (라플라스 변환) (0) | 2024.02.20 |
| 04 forced response 09 (강제 응답) (0) | 2024.02.10 |
| 04 forced response 06 , 07 (강제 응답) (1) | 2024.02.03 |
| 04 forced response 05 (강제 응답) (0) | 2024.02.03 |