
filtering이 된다는 것은 LTI System인 H 를 구했을 때 k 에따라 (ak, w0k 가 fourier series에 index임으로) amplitude 가 달라짐을 의미한다.

input 함수의 T를 높여서 frequency 를 늘리니까 H의 값 (즉 amplitude) 이 frequency가 클수록 감소되는 양상을 보인다.
즉 고주파 input들은 값이 줄어들게 된것이다.
input은 빨간색 사각형 주기함수인데 실제로 LTI를 거쳐서 나오는 output은 모양을 달리 띄게 된다.
주로 저 직각 부분에 frequency가 높은 부분이라 output이 잘 따라오지 못하는 양상을 띄게 된다.

y는 x의 주기 (ejwt)와 같고 phase, amplitude만 달라지기에 저렇게 놓고 식을 전개할 수 있다.
이때 H 절대값을 보면 w와 반비례 하는것을 볼 수 있다. 즉 이 LTI에서는 w(각속도, 진동수) 가 높을 수록 값이 줄어듬으로
고주파 진동수가 filtering 된다는것을 알 수 있다.
Response to General Input (in Frequency)

주기가 없는 함수도 마치 무한대의 주기를 갖는것처럼 간주해서 주기함수라고 일종의 trick을 쓸 수 있다.

한 주기에 대해 적분 하면 되니 -T/2 ~ T/2 사이로 한 것이다.
또한 -S ~ S 사이는 T/2 사이에 있고 이 구간에서 함수는 1이다.

T가 증가할 수록 w0는 줄어들게 된다.
그래프에서 k는 일정한 정수배이고 w0가 줄어드니 점점 Tak 의 간격이 촘촘 해지는것을 볼 수 있다.
T가 극한으로 가면 discrete 에서 continous 하게 frequency compoenent 들이 분포하게 된다.
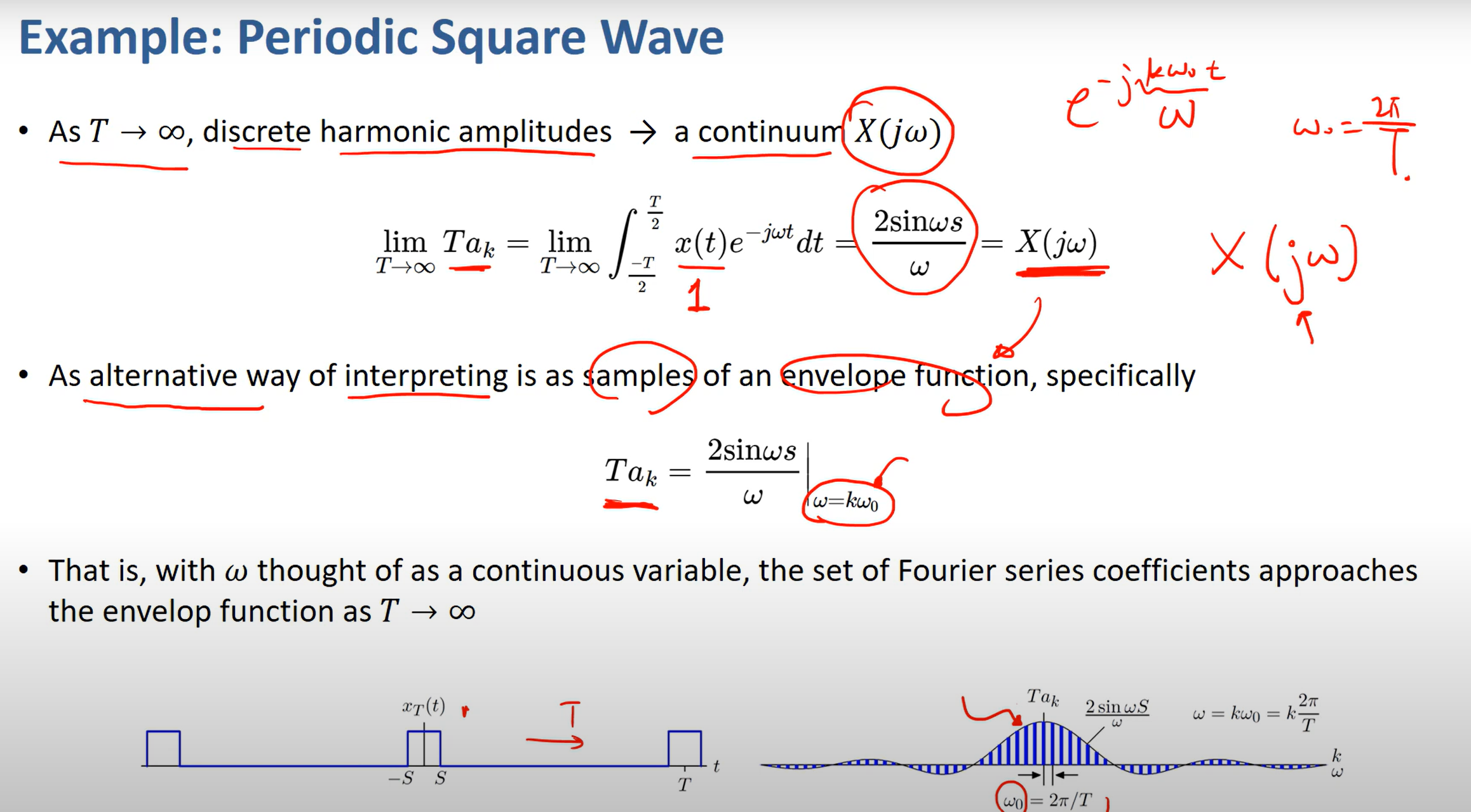
위에서 한것처럼 discrete -> continous 하게 frequency 들이 존재한다고 봐도 되지만 역으로
주기가 작을 때는 continuous 한것에서 몇개를 sampling 한것으로 봐도 된다.
'AI > Dynamical Systems (동적시스템)' 카테고리의 다른 글
| 05 Laplace transform 03 (라플라스 변환) (0) | 2024.03.02 |
|---|---|
| 05 Laplace transform 01, 02 (라플라스 변환) (0) | 2024.02.20 |
| 04 forced response 09 (강제 응답) (0) | 2024.02.10 |
| 04 forced response 08 (강제 응답) (1) | 2024.02.06 |
| 04 forced response 05 (강제 응답) (0) | 2024.02.03 |