lossi 를 표현한 그래프가 굉장히 보기가 어렵다.
plt.plot(lossi)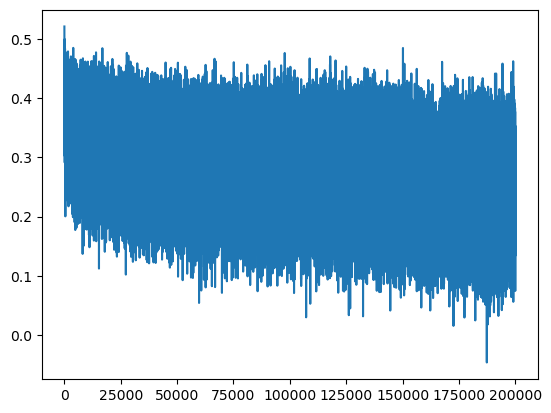
plt.plot(torch.tensor(lossi).view(-1, 1000).mean(1))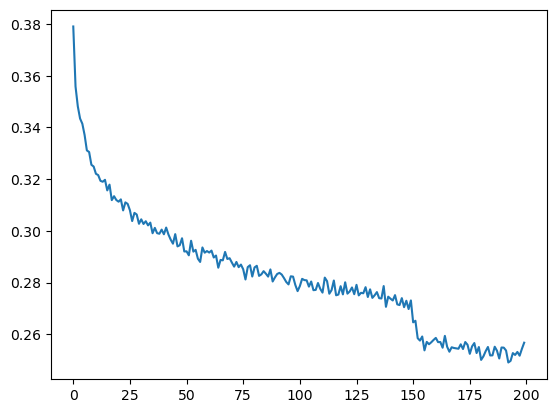
(200,1000) 으로 만든후에 row를 기준으로 평균을 내어 loss decay가 일어난곳을 좀 더 명확히 확인 할 수 있다.
class Embedding:
def __init__(self, num_embeddings, embedding_dim):
self.weight = torch.randn((num_embeddings, embedding_dim))
def __call__(self, IX):
self.out = self.weight[IX]
return self.out
def parameters(self):
return [self.weight]emb = C[Xb]를 클래스로 추상화한 것이다.
class FlattenConsecutive:
def __init__(self, n):
self.n = n
def __call__(self, x):
B, T, C = x.shape
x = x.view(B, T//self.n, C*self.n)
if x.shape[1] == 1:
x = x.squeeze(1)
self.out = x
return self.out
def parameters(self):
return []x = emb.view(emb.shape[0], -1) #concatenate the vectors를 추상화한 것이다.
# Near copy paste of the layers we have developed in Part 3
# -----------------------------------------------------------------------------------------------
class Linear:
def __init__(self, fan_in, fan_out, bias=True):
self.weight = torch.randn((fan_in, fan_out)) / fan_in**0.5 # note: kaiming init
self.bias = torch.zeros(fan_out) if bias else None
def __call__(self, x):
self.out = x @ self.weight
if self.bias is not None:
self.out += self.bias
return self.out
def parameters(self):
return [self.weight] + ([] if self.bias is None else [self.bias])
# -----------------------------------------------------------------------------------------------
class BatchNorm1d:
def __init__(self, dim, eps=1e-5, momentum=0.1):
self.eps = eps
self.momentum = momentum
self.training = True
# parameters (trained with backprop)
self.gamma = torch.ones(dim)
self.beta = torch.zeros(dim)
# buffers (trained with a running 'momentum update')
self.running_mean = torch.zeros(dim)
self.running_var = torch.ones(dim)
def __call__(self, x):
# calculate the forward pass
if self.training:
if x.ndim == 2:
dim = 0
elif x.ndim == 3:
dim = (0,1)
xmean = x.mean(dim, keepdim=True) # batch mean
xvar = x.var(dim, keepdim=True) # batch variance
else:
xmean = self.running_mean
xvar = self.running_var
xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # normalize to unit variance
self.out = self.gamma * xhat + self.beta
# update the buffers
if self.training:
with torch.no_grad():
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * xmean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * xvar
return self.out
def parameters(self):
return [self.gamma, self.beta]
# -----------------------------------------------------------------------------------------------
class Tanh:
def __call__(self, x):
self.out = torch.tanh(x)
return self.out
def parameters(self):
return []
# -----------------------------------------------------------------------------------------------
class Embedding:
def __init__(self, num_embeddings, embedding_dim):
self.weight = torch.randn((num_embeddings, embedding_dim))
def __call__(self, IX):
self.out = self.weight[IX]
return self.out
def parameters(self):
return [self.weight]
# -----------------------------------------------------------------------------------------------
class FlattenConsecutive:
def __init__(self, n):
self.n = n
def __call__(self, x):
B, T, C = x.shape
x = x.view(B, T//self.n, C*self.n)
if x.shape[1] == 1:
x = x.squeeze(1)
self.out = x
return self.out
def parameters(self):
return []
# -----------------------------------------------------------------------------------------------
class Sequential:
def __init__(self, layers):
self.layers = layers
def __call__(self, x):
for layer in self.layers:
x = layer(x)
self.out = x
return self.out
def parameters(self):
# get parameters of all layers and stretch them out into one list
return [p for layer in self.layers for p in layer.parameters()]추상화가 이뤄져서 좀더 손쉽게 모델링이 가능해졌다.
# hierarchical network
n_embd = 24 # the dimensionality of the character embedding vectors
n_hidden = 128 # the number of neurons in the hidden layer of the MLP
model = Sequential([
Embedding(vocab_size, n_embd),
FlattenConsecutive(2), Linear(n_embd * 2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
FlattenConsecutive(2), Linear(n_hidden*2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
FlattenConsecutive(2), Linear(n_hidden*2, n_hidden, bias=False), BatchNorm1d(n_hidden), Tanh(),
Linear(n_hidden, vocab_size),
])
# parameter init
with torch.no_grad():
model.layers[-1].weight *= 0.1 # last layer make less confident
parameters = model.parameters()
print(sum(p.nelement() for p in parameters)) # number of parameters in total
for p in parameters:
p.requires_grad = True실제 inference 할때는 batchnorm1d를 training을 false로 해줘야한다.
running mean, var 으로 전 강의에서 봤던 normal distribution유지하기 기법을 쓰고싶기 때문이다.
training을 켜두면 torch.var(int) 가 들어와서 nan의 결과값을 던지게 됨으로 에러가 발생함
단순 1개의 int의 variance를 구하는것은 말이 안되기 때문이다.
overview of Wave net
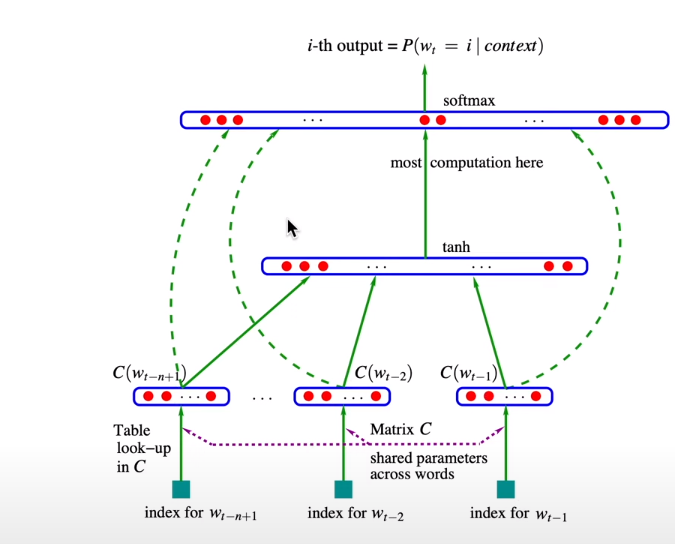
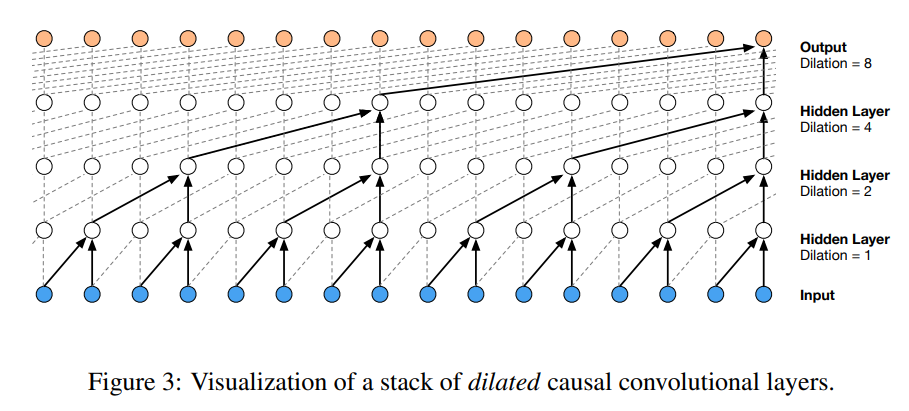
모델 스케일을 늘리기 위해서기존 모델에서 layer를 더 추가하거나 아니면 layer에 노드를 더 추가하는 방법은 좋지 않다.
모든 input들을 한번에 하나의 레이어로 squash 하는것은 좋지 않기 때문이다.
wave net은 layer를 지날때마다 input들을 하나하나 추가함으로 위의 단점을 완화 시켜줄 수 있다.
........ --> y
.......y --> u
......yu --> h
.....yuh --> e
....yuhe --> n
...yuhen --> g
..yuheng --> .이제 input block size를 늘려서 8개씩 가져온다. 단순히 증가시키는것만으로 loss를 감소시켜 주긴 한다.
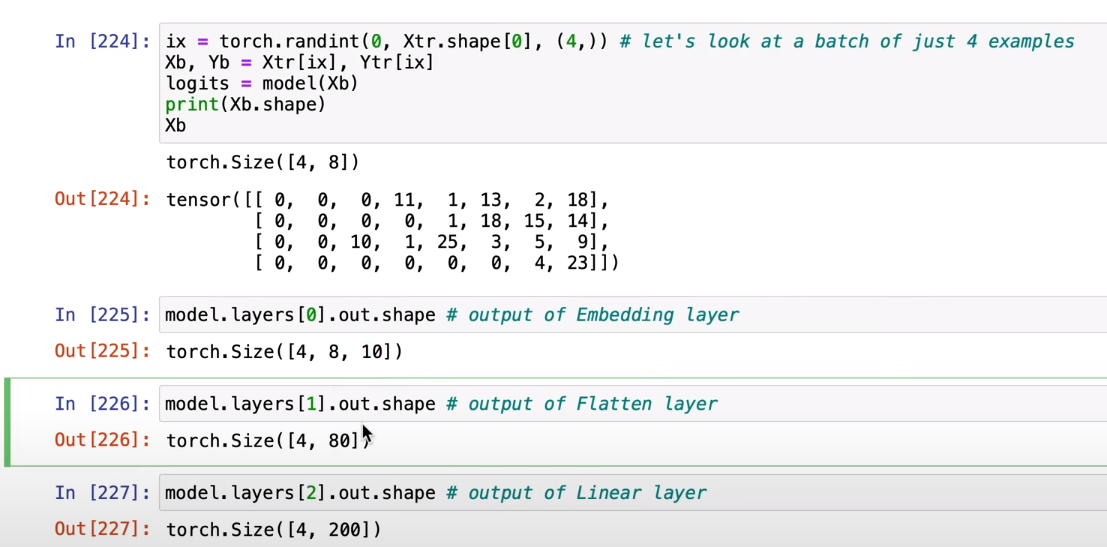
4개의 예시이고 각 예시의 단어 갯수는 8개까지 이제 수집하고
그리고 embedding layer는 원래 각 예시의 단어 각각을 10차원에 embedding하였다.
현재 Lienar layer가 200개 뉴런이 있는것이다.

pytorch matrix multiple 은 last tensor(80)에만 적용이 되고 나머지 dimension은 변하지 않는다.
이것을 활용해서 기존의 예시들의 단어갯수가 8개씩 들어오는것을 한번에 flatten 해서 80으로 처리해서 matrix multiple을 하는것이 아니라 각각 2개의 그룹으로 묶어서 일종의 배치로 처리되게 하고 싶다.

4개의 예시, 4개의 그룹 , 각 그룹안의 2개 단어갯수 * 10 dimension embedding
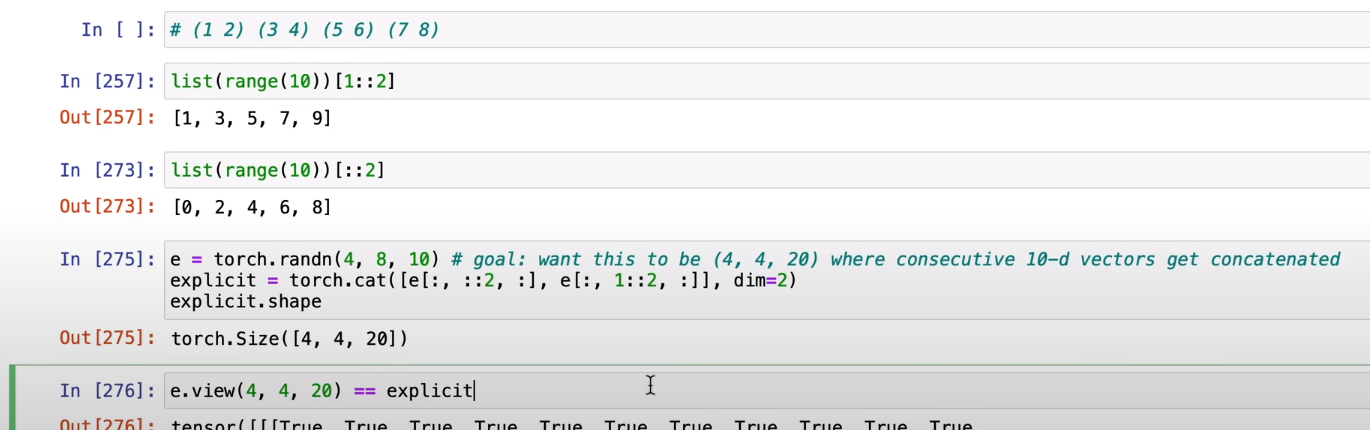
2번째 torch 차원에서(8) 짝수 번째 만 뺴오고 그다음에는 홀 수 번 째 만 빼온 후에 그 둘을 concatenate 하는데 2번째 torch 자원 기준으로 합친다.
하지만 그냥 view(4,4,20)으로 위와 동일한 효과를 준다. 위의 FlattenConsecutive 가 이것을 기반으로 구현된것이다.
B,T,C = 4, 8, 10 으로 n = 2인 형태가 위와 같다.

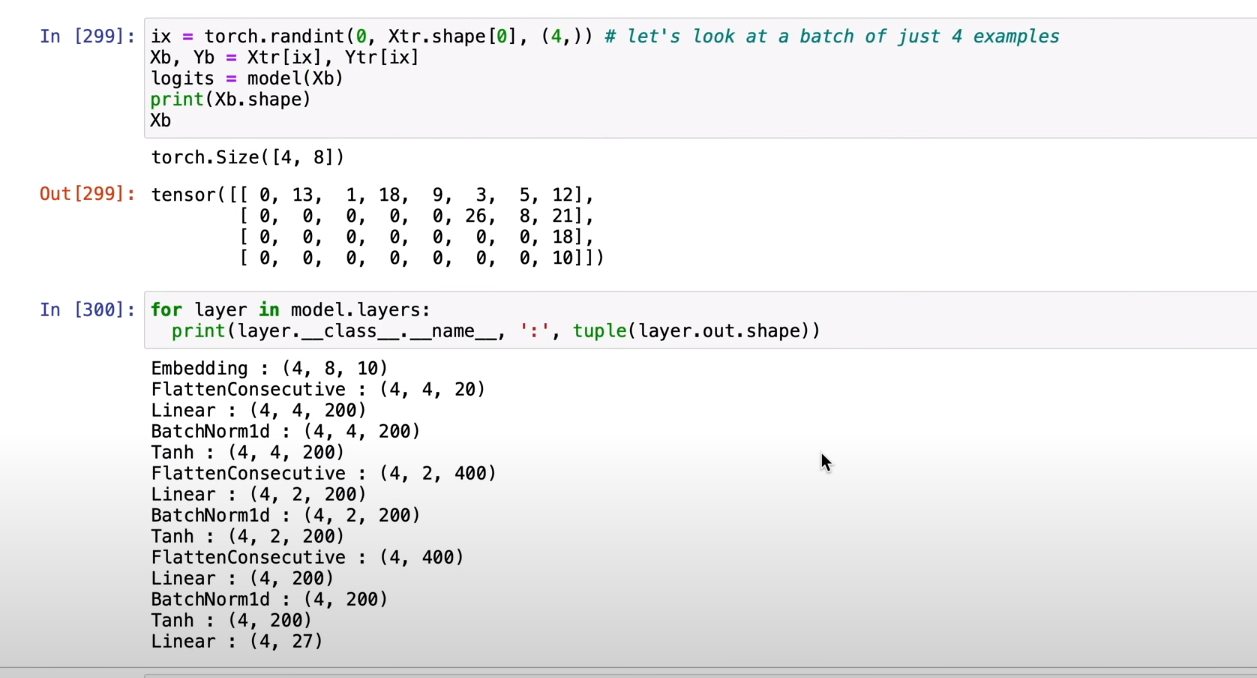
첫번쨰 Flatten Consecutive (4,4,20) @ Linear(20,200) = (4,4,200) 이 나온것
두번째 Flatten Consecutive (4, 2, 2*200) @ Linear (2 * 200 ,200) 이 나온것이다. 아래 그림상으로

사진에는 16개의 input이지만 우리의 예시는 8이고 각 hidden layer에 2개 씩 그룹 지어 들어가는것은 똑같다.
첫번쨰 hidden layer output은 (4,4,200) tensor 이지만 이것을 2개씩 묶어서 하나의 hidden layer output으로 들어가야함으로 다시 2개씩 쪼개서 (4, 2, 2*200) @ (2 * 200 , 200) 으로 처리된것이다.
fixing batch norm 1d bug
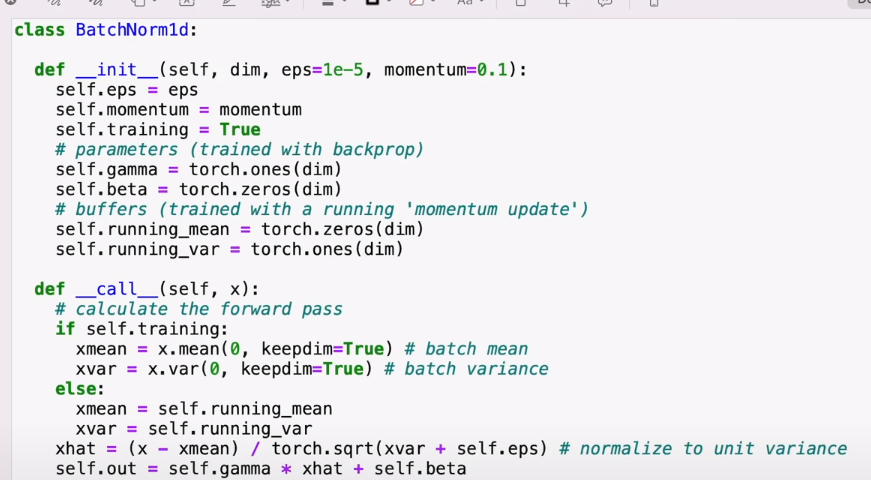
기존에는 input이 2차원임을 가정하고 0번쨰 차원을 기준으로 mean, var를 구하였는데
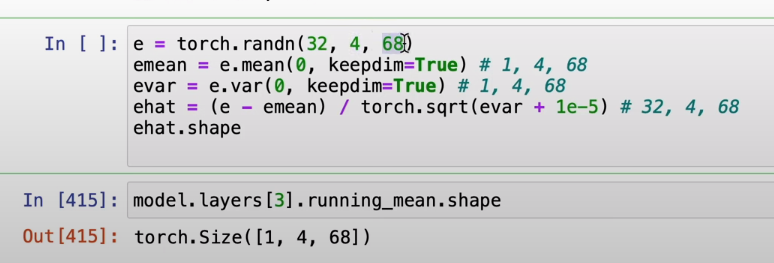
3차원이 들어와서 우리는 32*4 들의 평균을 구하고 싶은데 0차원 기준으로 평균을 구하니 (1,4,68) 이 남아서 의도한대로 동작하지 않게 된다.
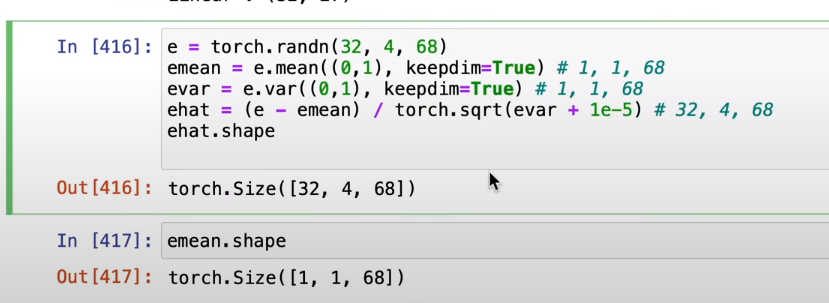
1차원도 추가해줌으로서 의도한 대로 동작하게 할 수 있다.
'AI > Andrej Karpathy' 카테고리의 다른 글
| Let's build GPT: from scratch, in code, spelled out. (0) | 2023.11.26 |
|---|---|
| Building makemore Part 4: Becoming a Backprop Ninja (0) | 2023.02.26 |
| Building makemore Part 3: Activations & Gradients, BatchNorm (0) | 2023.02.19 |
| Building makemore Part 2: MLP (0) | 2023.02.04 |
| The spelled-out intro to language modeling: building makemore (0) | 2023.01.24 |