Dp notions
1. Characterize the structure of an optimal solution
2. Recursively define the value of an optimal solution based on optimal solutions of subproblems.
3. compute the value of an optimal solution in bottom up fashion(recursion and memoization)
4. construct an optimal solution form the computed information
Longest Palindromic Sequence
Definition = A palindorm is a string that is unchanged when reversed
x = "underqualified"
def dp(i,j):
if i == j:
return 1
if x[i] == x[j]:
if i+1 == j:
return 2
else:
return 2 + dp(i+1,j-1)
else:
return max(dp(i+1,j), dp(i,j-1))
answer = dp(0,len(x)-1)
print(answer)We start by checking if the words on both ends are equal, and if not, we repeat by truncating one of the ends.

this implementation is without memoization so it takes exponential time
x = "underqualified"
L = [[-1 for _ in range(len(x))] for _ in range(len(x))]
def dp(i,j):
if L[i][j] != -1:
return L[i][j]
if i == j:
L[i][j] = 1
return 1
if x[i] == x[j]:
if i+1 == j:
L[i+1][j] = 2
return 2
else:
return 2 + dp(i+1,j-1)
else:
L[i][j] = max(dp(i+1,j), dp(i,j-1))
return L[i][j]using lookup array we can reduce time , taking theta n squared time
where n^2 is number of subproblems and 1 for to solve each subprobelm , given that smaller ones are solved.
Optimal BSTs

root node's depth is zero but there is plus 1 in formula.
W can be think as search probability(by client who use this tree, more common) of specific Key K.
try greedy = pick Kr that has W , for example highest go to root node

if Kr is largest key than we are going to have very unbalanced tree


counter example for greedy
Dp

e(i,j) = cost of optimal BST on Ki, Ki+1 ... Kj
r = root node

reason for adding W(i,j) is to show that +1 depth ,
alternating coins
first player always win or tie
compute odd order coin and even order coins sum and your guarantee to win when whole length of coin is even.
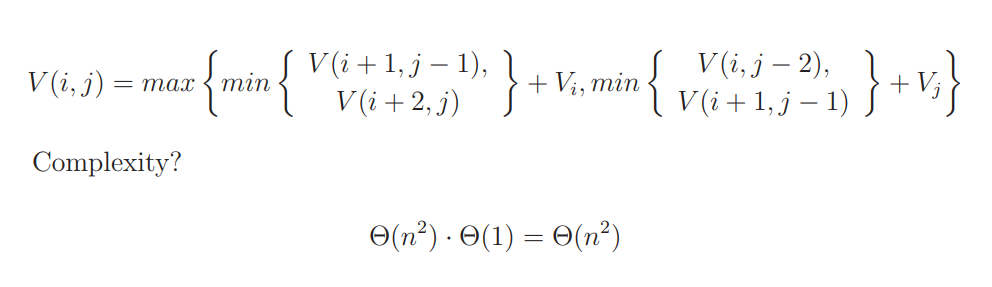
min is for opponent
'Algorithm > Design and Analysis of Algorithms' 카테고리의 다른 글
| Augmentation: Range Trees , B-Tree (0) | 2021.10.14 |
|---|---|
| Randomization: Universal & Perfect Hashing (0) | 2021.06.04 |
| Randomization: Skip Lists (0) | 2021.05.24 |
| Randomization: Matrix Multiply Checker, Quicksort (0) | 2021.05.19 |
| Text justification (0) | 2021.01.24 |