Finger Search Tree (level link 2-3 tree and store keys in leafs)
if we have already node y we want to search x from y in O(lg |rank(y) - rank(x)| ) time.

beside leaf nodes every node contains min and max. e.g) left most == min(1) max(7) , top == min(1) , max(9)

every iteration we go up by 1 level.
at N iteration we we will skipping roughly 2^N or 3^N since it is 2-3 tree.
if abs(rank(x) - rank(y)) = k , then N is going to be logk
Range Tree (used in DB index)
here db's columns are same as dimension
Qustion = we want to search ranges for given queries

these are 2d and 3d cases , rectangles are queries.
in 1D case we preprocess our element in Perfect Binary Search Tree.

assume we want to search a from b
1. while we walk up from a whenever we get right parent we want that node and subtree to the right.
2. whille we walk up from b whenever we get left parent we want that node and subtree to the left.
we do this repeatly and alternately until we meet at the top
it takes about 2*logn = O(logn)
in 2d case
project every point on to the x axis. and to above algorithm like in 1d case.

but some of them are out of range of query(blue box).

now we do same 1d case with y projection and make blue range tree.
blue tree satisfy query condition.
total time takes O(log^2 N) time.

total space takes nlog^(d-1) n. because duplicate key 'k' , for example , only happens logn times. so for every dimension our space become large as log factor.
https://www.youtube.com/watch?v=aZjYr87r1b8&ab_channel=AbdulBari

B Tree = at every key it has recordpointer, and child pointer represent a block pointer.
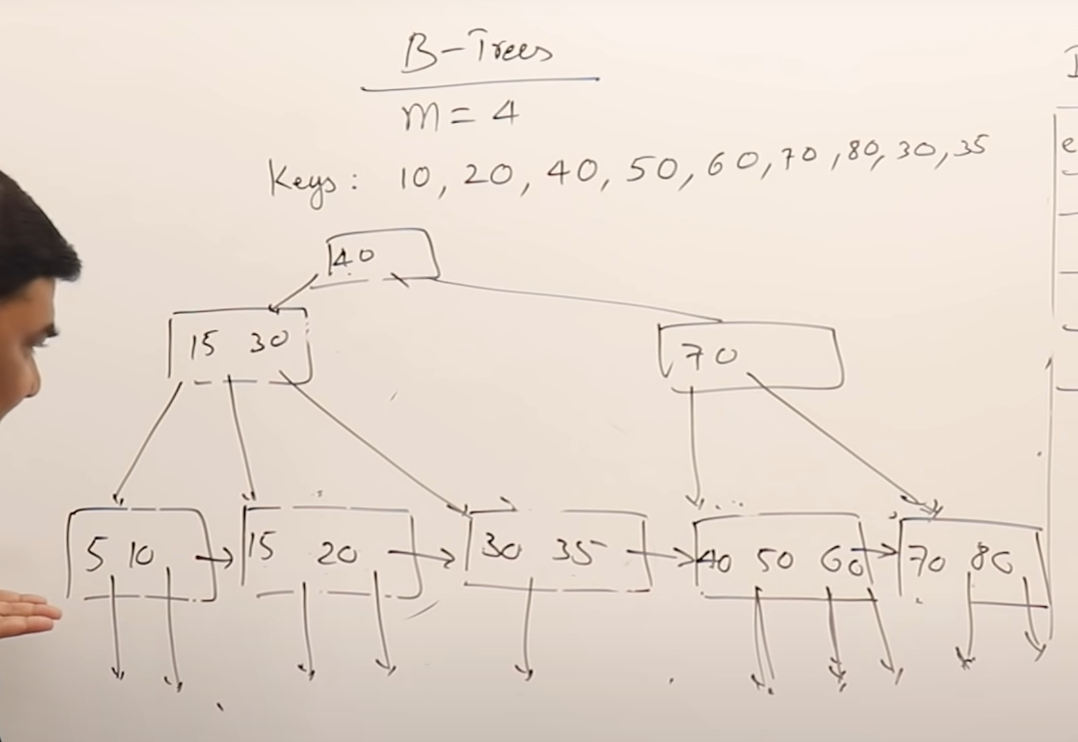
B+ Tree = same as B Tree , every key has it's recordpointer but not on the same level node , but on leaf node
which is more like dense index ,
'Algorithm > Design and Analysis of Algorithms' 카테고리의 다른 글
| Dynamic Programming: Advanced DP (0) | 2021.11.07 |
|---|---|
| Randomization: Universal & Perfect Hashing (0) | 2021.06.04 |
| Randomization: Skip Lists (0) | 2021.05.24 |
| Randomization: Matrix Multiply Checker, Quicksort (0) | 2021.05.19 |
| Text justification (0) | 2021.01.24 |