Matrix Multiply Checker
AB = C takes at least

these much time. we want matrix product checker that checks if mutiplication is correct in O(n2).
we choose vector r randomly that has only 1 or 0. and we compute A(Br) = (Cr) if it is same than we say it's true otherwise false. this computation takes O(n2) because (n*n) * (n*n) * (n*1) == n^2 , (n*n) * (n*1) == n
we want to show that there are many r such that ABr != Cr.
If AB != C then Pr[ABr != Cr] >= 1/2 this means checker will give false postive , but when you keep checking multiple time you can reduce your wrongess by half every time
Claim = If AB != C then Prob[ABr != Cr ] >= 1/2 == meaning that probability that r will find incorrectness of mutiplication is greater than half.
we want to show that there are many r such that Dr != 0 == meaning ABr != Cr
assume AB - C = D and at least 1 entry of D is not zero.
but there are bad r that even though AB - C != 0 , when mutiplied by r will produce ABr -Cr = 0 whichi is false positive. D != 0 but Dr = 0
we can always make bad r to good r when we know Dij that is not equal to zero and we can just plus 1 to jth in bad r and make it to good r which tells if D = 0 then Dr = 0.
r` = r + v , r` is good r because D(r+v) = Dr + Dv = 0 + nonzero.
v is vector that has 1 in jth position which will be mutiply by nonzero Dij.
we can notice that there is 1 to 1 mapping with good r(r`) and bad r and we can now argue that #good r >= #bad r
and finally we have Pr[Dr != 0 ] >= 1/2 and by having this we can keep checking mutiple time and reduce the probaility of getting wrong output.
Quick sort
picking pivot smartly is important otherwise we get worstcase analysis O(n2).
pick median of median as pivot. Convex Hull , Median Find (tistory.com)
Convex Hull , Median Find
Convex Hull S = {(xi, yi)|i = 1, 2,...,n} assume no two have same x coordinate, no two have same y coordinate, and no three in a line for convenience Convex Hull ( CH(S) ) == smallest convex polygon..
tonylim.tistory.com
this is bad because we are doing recursive call(median find) inside recursive call(quick sort).
we do paranoid quick sort which use random pick unitl it find almost median like below
since it is paranoid it will keep try peeking pivots until we get good pivot.

since probaility of picking good pivots is almost half(1/2) the expected number of random pick is 2. and we get recursion forumla like below
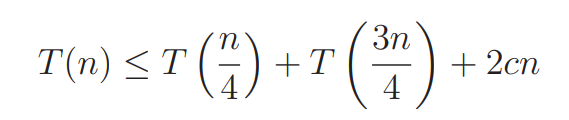
and with tree

tree height can be at most log4/3(2cn) == right side of tree
takes O(nlogn)
reference ==
'Algorithm > Design and Analysis of Algorithms' 카테고리의 다른 글
| Randomization: Universal & Perfect Hashing (0) | 2021.06.04 |
|---|---|
| Randomization: Skip Lists (0) | 2021.05.24 |
| Text justification (0) | 2021.01.24 |
| Graph Transform (0) | 2021.01.11 |
| Dijkstra , bellman-ford ,Bi-directional Djikstra (0) | 2021.01.05 |