Convex Hull , Median Find

Convex Hull

S = {(xi, yi)|i = 1, 2,...,n} assume no two have same x coordinate, no two have same y coordinate, and no three in a line for convenience

Convex Hull ( CH(S) ) == smallest convex polygon containing all points in S

polygon cannot be smaller than this

represented by the sequence of points on the boundary in order clockwise as doubly linked list

Brute force

Test each line segment to see if it makes up an edge of the convex hull

• If the rest of the points are on one side of the segment, the segment is on the convex hull

• else the segment is not.

O(n2) edges, O(n) tests ⇒ O(n3) complexity

Divide and Conquer Convex Hull

Sort points by x coord (once and for all, O(n logn ) )

For input set S of points:

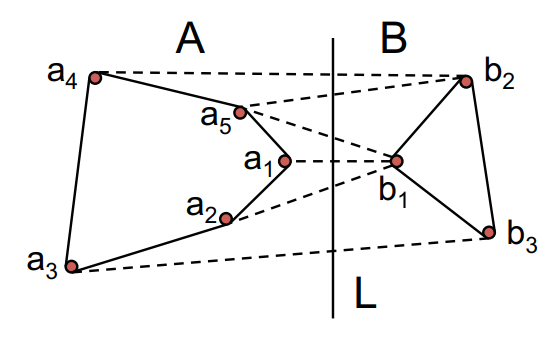
• Divide into left half A and right half B by x coords

• Compute CH(A) and CH(B)

• Combine CH’s of two halves (merge step)

 

L 과 만나는 선이 y(i,j) (upper tangent , lower tangent)        Merge == O(N^2) look all pairs

  better algorithm so called "finger line algorithm" , need to see demonstartion
== 2. Divide & Conquer: Convex Hull, Median Finding - YouTube

left side = counter clockwise , right side = clockwise  //

pseudo algorithm 

to represent new convex hull(merged one) , we just walk thorough upper tangent to lower tangent
a3(upper) b1 b2 b3 b4(lower) a1 a2  == O(N)

Median Finding

Given set of n numbers, define rank(x) as number of numbers in the set that are ≤ x.
Find element of rank  FLOOR((n+1)/2)(lower median) and CEIL((n+1)/2)(upper median).

i - k because we are looking for rank in whole thing not just in C subset

recur through B and C

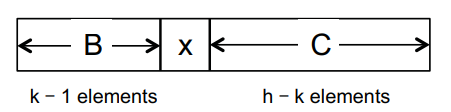
but picking x might be extremly unbalance! == O(N^2)   How do we pick cleverly? we want determinstic fairly balanced partition 

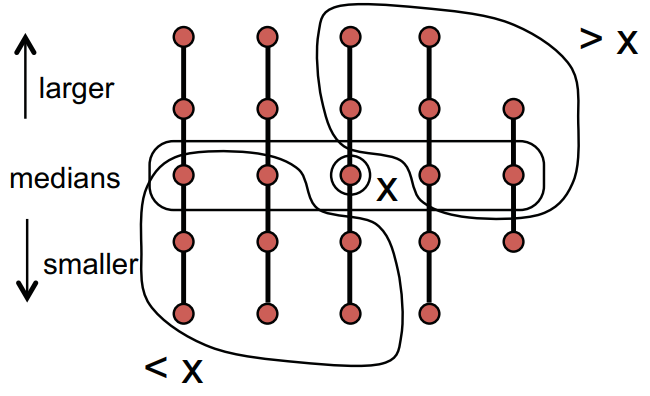
Picking x Cleverly

Need to pick x so rank(x) is not extreme.

• Arrange S into columns of size 5 ( CEIL (n/5) cols)

• Sort each column (bigger elements on top) (linear time) , only 5 element

• Find “median of medians” as x

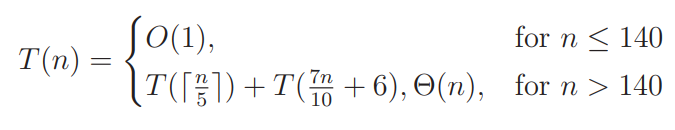
T(n/5) == finding median of median using SELECT algorithm,

T(7n/10 +6) == n - half( 3( n/10 -2) ) elements , O(N) == sorting whole cloumn