
in ML Quantization usually mean FP32 -> INT8
Usually, when the training of the model is finished, train parameters falls in to simple shallow distribution.

scale ? zero-point ? how do i calculate that scale? Z = 207 so we can map 2^b - 1 to 256. S = 0.6/255

Linear depends on function , symmetric asymmetric depends on starting point ( 0 == symmetric , otherwise asymmetric)

Dequantization cannot reproduce acutal value 100% , it has some errors, and we want to minimize that errors
Rounding error occurs when a continuous value (often a floating-point number) is converted to a discrete value (often an integer) by rounding.
Clipping error arises when the value to be quantized exceeds the range that can be represented by the quantization levels

think of Scale factor as step size, because if you choose larger scale factor due to large range(r_min ~r_max)
of real value , it will increase the round errors.
on the other hand if you can choose scale factor smaller due to small range of real value , it will decrease the round errors
but decreasing (r_min~ r_max) can lead increasing of clipping error

stochastic == round up , down randomly

symmetric == meaning zero points are zero
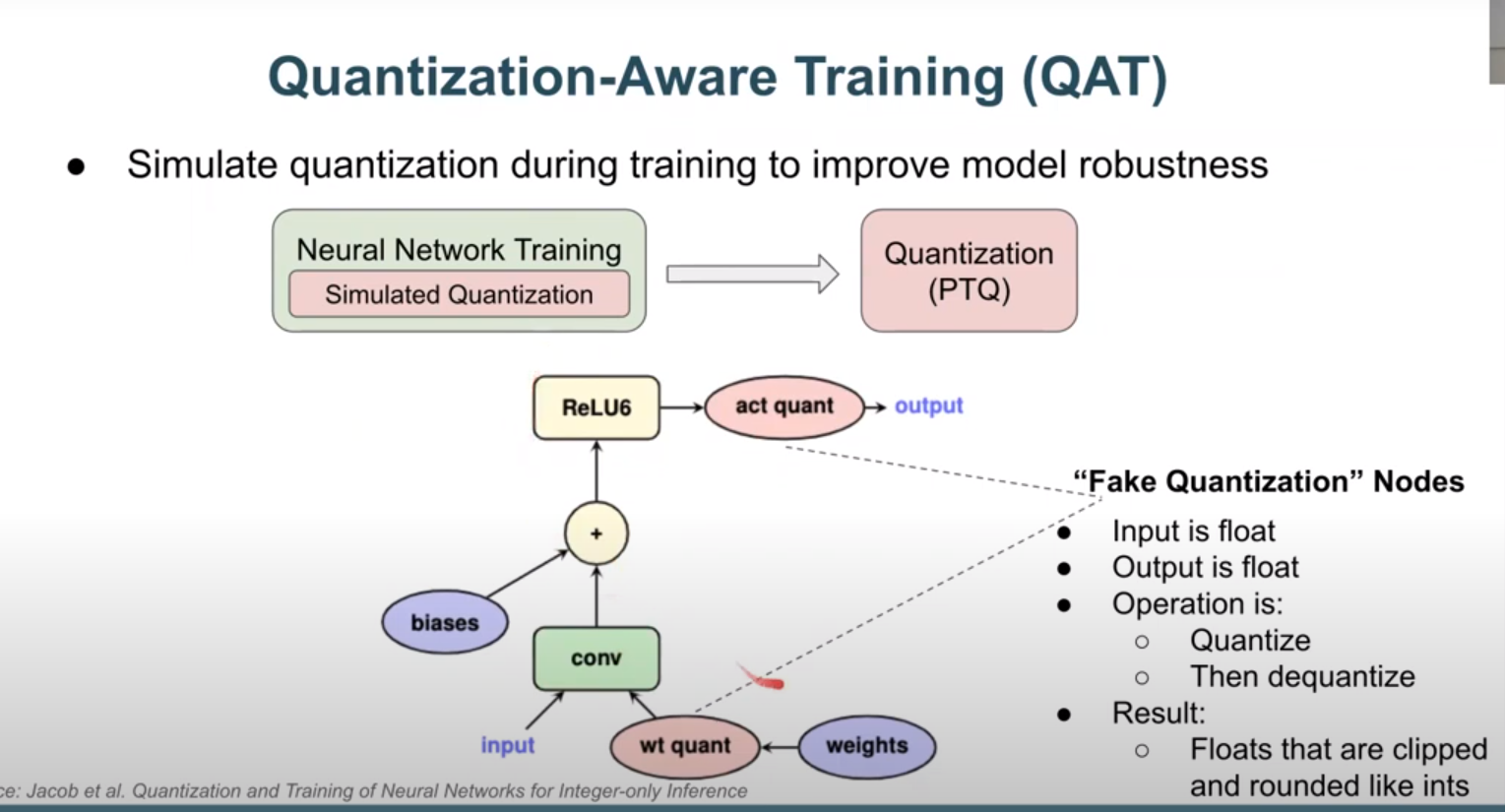
Wq is constant because we are assuming inference time, which means we don't change weights
to eliminate online overhead, we can use symmetric quantization only for weights , which makes Zw == 0

weights are forzen and don't change, can precompute scale and zero point ,but not with inputs/activation
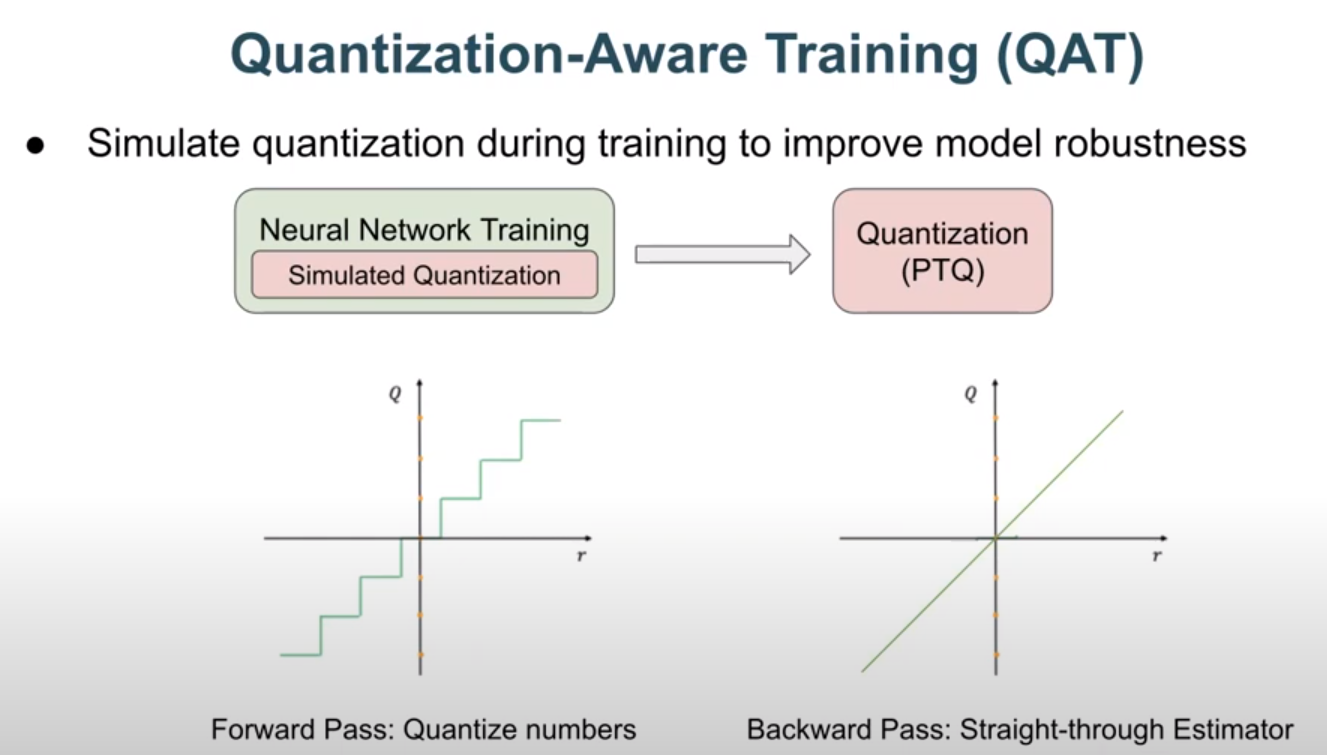
- Forward Pass: During the forward pass, the non-differentiable function (e.g., a step function that binarizes values) is applied as usual.
- Backward Pass: During the backward pass, the gradient is computed as if the function were an identity function, effectively treating the non-differentiable operation as if it were linear.

unlike randomly removing weight, we now have some criteria , General formulation is to check which weight(neuron) has most least changes in loss function.
but doing it to every billion parameter is interactable. so approximate
'Computer Architecture > Cornell ECE 5545' 카테고리의 다른 글
| ML HW & Systems. Lecture 5: Microarchitecture (0) | 2024.07.06 |
|---|